Alexander’s short note on the Synchrotron Light

Synchrotrons are the most efficient known devices for generating high flux, high energy X-ray beams. The principle is to accelerate electrons to velocities approaching the speed of light, and bend their path using a powerful magnet. This causes the electron to emit energy in the form of a coherent beam of photons within a very small solid angle which scales with the relativistic factor b=(1-v2/c2)1/2.

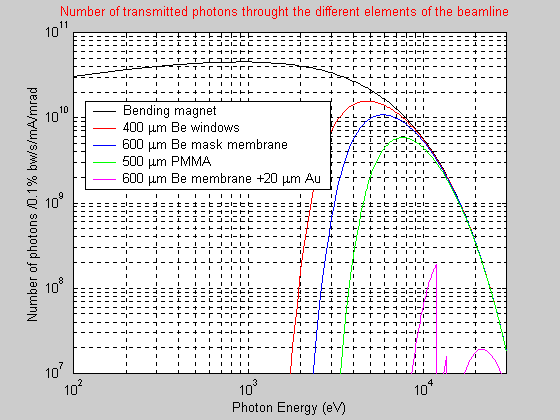
Electron energy in the ring scales inversely with b. In a synchrotron it is progressively accelerated from rest (energy of about 0.5MeV) to many times that value (run the applet above to see). It is important to synchronise the magnetic field strength with the electron velocity, hence the term 'synchrotron'. To achieve that, it is convenient to push electron into bunches by using radio frequency pulses (you should be able to figure out why). 



Key components of any machine are: a linear accelerator (linac), booster and storage rings, bending magnets and RF cavities. At SRS Daresbury the storage ring energy is 2GeV, at the ESRF 6GeV, while DIAMOND will be a 3GeV machine. 


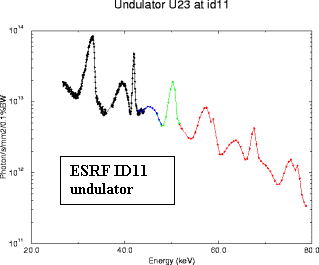
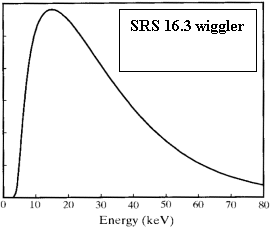
The ring energy affects the characteristic, or critical energy of X-rays produced by the bending magnets, as well as the magnetic field in the gap (see example spectrum above from BM10 on the 2GeV Elettra in Trieste – no useful photons above 30keV). However, more efficient devices like multipole wigglers and undulators can produce more energetic X-rays from the same electrons.


SRS station 16.3 is a high-resolution/high-energy diffraction facility, suitable for a wide range of applications in physics and materials science. 16.3 occupies the central beamline of wiggler16, a 6T superconducting wavelength-shifter. At 16 keV it has the highest critical energy of all the SRS stations. Energies from 5 KeV to above 70 KeV are available, and the spectrum is very smooth as shown in the figure. 

Whereas wiggler uses a line of alternating magnetic diploes, an undulator imposes an even more complex field variation. The result is very powerful emission of X-ray at chosen resonance energies. The spectrum of such a device is rather ‘choppy’, as illustrated in the case of ID11 on ESRF in the picture. If you are after maximising monochromatic flux, this is the best option. There is aprice to pay: if you ‘drop’ off the peak, the flux drops too. As a consequence, continuous monochromator adjustment is necessary.

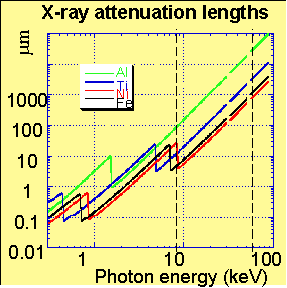
For many materials engineering problems having access to energies above 30-40keV is essential. The picture on the left shows X-ray attenuation lengths (in mm) for Al, Ti, Ni and Fe as a function of photon energy. Above 60keV transmission experiments through millimetres of these important structural materials become possible.

There are essentially two modes for diffraction experimentation: fixed energy (monochromatic) and resolving angle, or fixed angle and resolving energy (energy-dispersive). We can measure angles to the accuracy of 10-6 quite routinely, so monochromatic mode is preferred for high resolution work. We can discriminate energy only to about 10-2, which makes energy-dispersive mode sound like a non-starter. That is not so for strain measurement, though: we can find peak centres to accuracy which is many orders better than a channel width, so 50 microstrain accuracy can be achieved.

Depending on the problem, one or the other mode (mono or EDX) may be preferred. What is important is to have the flexibility allowing both modes to be accessed.

The other important aspect of beamline design is space management. Traditional diffractometers impose too much constraint on the sample space, as we know from SRS16.3, ID11 and BM16. A more sample-centred design would consist of a manipulation table surrounded by movable detectors which can be introduced and aligned as required by the experiment. It would also guarantee that the interest of any group interested in high energy X-ray diffraction can be satisfied.

alexander.korsunsky@eng.ox.ac.uk

September 2001