Data Analysis for Neuroscientists III:
Standardized Scores

How unusual is my sample? Let's start by generating two simulated 'datasets' iq and h with 1000 data points in each: iq - drawn from a Normal distribution with mean 100 and standard deviation 15 h - drawn from a Normal distribution with mean 179cm and standard deviation 7cm These are the true statistics for English men You can do this using the function randn which generates normally-distributed random numbers with a mean of 0 and a standard deviation of 1 HINT If you can't figure out how to change the mean and standard deviation, there is an example in: >> help randn ? >> iq = 100 + randn(1000,1).*15 >> h = 179 + randn(1000,1).*7 Now then. Say we encounter a fine specimen of mankind, with height = 195cm and IQ = 130. Let's call him Eric. Which is more unusual, Eric's height or Eric's IQ?

Eric

Distance from the mean

How much higher is Eric's IQ (130) than the population mean?

?

>> iq_diff = 130-100

By the way, how would I use mean to compare Eric's IQ to the mean of the sample of 1000 men?

?

>> iq_diff = 130-mean(iq)

And why didn't I do that?

Because the question particularly asked how much taller Eric is than the population mean, not the sample mean!
By the way though, it is quite unusual that we happen to know the population mean in this case.

How much taller is Eric (height 195cm) than the population mean?

?

>> h_diff = 195-179

So we know that Eric is x IQ points higher than the population mean, and y cm taller than the population mean.
How can we compare these two values to figure out which is more unusual, his height or his IQ?

?

HINT: we need to find a common unit that tells us something about where a datapoint lies in the population distribution.

Standardized differences

What is the standard deviation of IQ scores in the population?
What is the population standard deviation of men's heights?

?

15 points and 7 cm respectively.

These population values were given earlier in the exercise, when you generated the "data".

How would you find the sample standard deviations?

?

>> std(iq)
>> std(h)

So how many standard deviations from the mean is Eric's height?

?

>> (195-179)/7

...and what about his IQ?

?

>> (130-100)/15

So which is more unusual?

?

His height, because his height is 2.3 standard deviations above the mean and his IQ is only 2.0 standard deviations above the mean.

Error bars

You will sometimes hear one scientist berating another for showing data without error bars.

In relation to the work you have just done, why do you think this is?

?

Well, one big reason is that a lot of measurements are in rather arbitrary units (for example, percentage of trials correct on some task in a psychology experiment, or the size of an electrical potential measured at the scalp).

So a raw deviation of the sample of interest (say, the size of an event-related potential after a surprising event is 5mV bigger than after non-surprising events) is pretty meaningless - but a score in terms of standard deviations (say, the ERP on surprising trials is 3 standard deviations above the mean) is instantly meaningful.

The Z score

Measuring the deviation of a sample in terms of how many standard deviations it is from the mean gives us a common currency for comparing how unusual samples are.

The number of (population) standard deviations a sample lies from the (population) mean is such a useful statistic that it has a name - the Z score.

Can you write down a formula for the Z-score?

?

HINT: It starts with Z = , and contains symbols for the value in question (x), the population mean (μ) and the population standard deviation (σ).

?

ANOTHER HINT: Think about what you typed into MATLAB to find out how many standard deviations from the mean Eric's height was.

?

The answer:

Z =	(x - μ)
	σ

The definition of the Z-score is the distance of a point x from the mean μ of a normal distribution, in units of the standard deviation of that normal distribution, σ

We can also think about the Z-score as 'mapping' a point in our data distribution to another, well known distribution - the Standard Normal Distribution.

The Standard Normal Distribution What is the mean Z-score for the 1000 Heights in our sample? What is the standard deviation of the Z-scores? ? >> z = (h-179)/7 >> mean(z) >> std(z) or you could have simply done: >> mean((h-179)/7) >> std((h-179)/7) Do the same for the 1000 IQ samples. What are the mean and standard deviation of the Z-scores in this case? Hopefully, you should have found that in both cases: The mean Z-score is about zero The standard deviation of Z-scores is about 1. Can you see why this is, from the equation for the Z-score? In fact, because out height and IQ data were normally distributed (we made them that way - remember we generated the "data" using using randn), the process of converting the height/IQ values to Z-scores transforms their distribution to another normal distribution, with mean = 0 and standard deviation = 1. This is called the Standard Normal Distribution. It is the distribution from which the function randn draws numbers. We can plot a Probability Density Function (PDF) for the standard Normal distribution using normpdf. 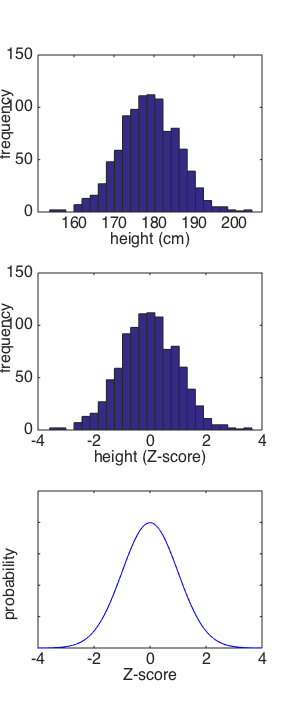DIVERSION - skip if short of time! and just look at this one instead --> HINT: Have you looked this? >> help normpdf Still not at all obvious how to plot the function? ? OK, let's break it down. First we need to decide on the range of Z-scores for which we want to plot the Standard Normal PDF. Let's say we want to plot the Standard Normal PDF for Z-scores between -4 and 4. Then we can make a vector containing those values: >> Z = [-4:4] and use normpdf to get the values of the PDF at those values of Z >> pZ = normpdf(Z,0,1) ... and then plot pZ against Z: >> plot(Z,pZ,'.-') Hmmm, that doesn't look like a nice Bell-shaped Normal distribution. You can make is smoother by plotting the function at more values of Z, eg try plotting it for Z-values with a spacing of 0.1 rather than 1 >> Z = [-4:0.1:4] ...etc as above ? Still confused about how to plot a function?? It might help to look at this example where we are plotting a more familiar function, y = x2. You may well have seen maths programs before which can plot functions like y = x2 directly from the equation. MATLAB doesn't work quite like that. It can't plot a function, only discrete value pairs like (x,y). So we need to give it some values of x in a vector x, >> x = [-4:4] ...and the corresponding values of y in a vector y      >> y = x.^2 and then plot the vector y against the vector x >> plot(x,y,'.-') ...by the way, the '.-' in the plot function means 'plot using dots at the actual values, and lines in between'. Now, the function y = x2 is actually continuous, so plotting a few pairs of (x,y) and joining them with straight lines is not a great approximation to the smooth curve we imagine for the graph of y = x2. MATLAB can only plot discrete values and join them with straight lines though, so to get a nice smooth-looking curve, the best option is just to plot a whole lot of values. For example, try using value of x spaced every 0.01 units rather than every 1 units. >> x = [-4:0.01:4] >> y = x.^2 >> plot(x,y,'.-') Have a look how smooth the curve looks now, if you don't plot the individual values: >> plot(x,y,'-') Right. After that diversion into the world of plotting graphs, let's take another look at that plot of the standard Normal distribution. And let's also compare that to the distribution of heights in our "sample" of 1000 men, and the distribution of Z-scores for heights. You can nicely see the distributions of those data if you plot a histogram of them using hist ? >> help hist I think you can tackle this one without me telling you the answer, right? What do you notice about the shape of the three distributions? ? All three distributions are the same shape. What about the values on the x-axis? ? The values on the x-axis should be the same for the standard Normal, and the histogram of Z-scores. You can actually think about the process of taking Z-scores (for Normal-distributed data) as transforming your data to a standard Normal distribution. More on why you would want to do this in a minute. What about the values on the y-axis? ? The values on the y-axis should be the same for the two histograms but different for the plot of normpdf. Why? What labels should we write on the y-axis in each case? ? In the histogram, each bar represents the number of men (out of 1000) with heights in a given range. If all the men were exactly the same height, how high would the corresponding bar be?      1000 In the PDF, we are plotting the probability of observing Z-scores of different values. The probability for all Z-values should add up to 1.0 (because a data point will certainly have some value between -∞ and +∞) If we were to plot a PDF for a probability distribution where there was only one possible value of the variable x, what would it look like?      A spike with y-value of 1.0

Probability of observing a given value Say I want to know how likely it is that if I test somebody's IQ, they will be at least as smart as Eric (who as you no doubt remember, had an IQ of 130). Last week, we calculated how many people in our sample had IQs of at least 130, using logical operators. Can you remember how to do this? How many people in the current "sample" have IQs of at least 130? Have a look at the histogram of raw IQ scores. How could you work out the proportion of subjects with IQs of at least 130 from this histogram? ? Add up the heights of the bars to the right of 130 on the x-axis, and divide by 1000 (to get the proportion, rather than the number of people with this IQ score). Now, by analogy, we can use the Standard Normal distribution to work out the probability that someone has an IQ of at least 130. First, we work out the Z-score corresponding to an IQ of 130. Then, we find the area under the curve, to the right of this Z-score. Because the area under the curve for the whole standard normal distribution adds up to 1, the proportion of it the right of a given Z-score gives the probability of observing a Z-score of at least this value, in the same way that the sum of the heights of the bars on the histogram gave the proportion of the 1000 men who have IQs of at least 130. Conveniently, MATLAB has a function that will work out the area under a normal distribution for you. It's called normcdf. Use normcdf to work out the probability of obtaining a Z-score of: Z > 3.1 Z < -1.96 Z > 2.3 Z < 2.3 ? HINT: as you may have realised from the help information, normcdf works out the area under the curve to the left of the given value. So if you want to find the probability of observing a Z-score at least as large as, say, 1.96, you are going to need to do 1-normcdf(1.96,0,1) Because the area under the curve to the left/right of these Z-scores tells us the probability of obtaining a Z-score at least that small/large, these areas define the p-values corresponding to those Z-scores. Hopefully, the Z-scores you just looked at correspond to some nice round-numbered p-values (you may need to round them to two significant figures). Which commonly used significance tests do the Z-values correspond to? Which actual values (in cm/ IQ points) do the Z-scores correspond to?

Interpretation of Z-scores

Here are the heights of some more men:

181 173 175 169 174 182 190 171 181 182

Work out their Z-scores, using only one line of code.

?

z = ([181 173 175 169 174 182 190 171 181 182] - 179)./7

Some of those Z-scores are negative! What does that mean?

?

HINT: you could get some insight by placing the heights and their Z-scores next to each other like this:

>> hsample = [181 173 175 169 174 182 190 171 181 182]'
>> z = (hsample-179)./7
>> [hsample z]

or you could even do this:

>> [hsample hsample-179 z]

?

The heights of the men with the negative Z-scores are below the mean.
So the signed Z-score tells you not only how far the sample is from the mean, but whether it is above or below the mean.

You might want to just glance back at the formula for the Z-score to appreciate why this happens.

Non-normal data

As you have seen, the Z-score relies on our ability to map our data onto the standard normal distribution, just by changing the values on the x-axis

What if the data are not normally distributed in the first place?

Reaction time data

Go to the website humanbenchmark.com and test your reaction time!

• I particularly like the high score board, on which the top two people have RTs of exactly 100ms
• This is ridiculously fast!
• US Navy Top Gun fighter pilots typically score between 200 and 225 milliseconds
• I think they programmed their computers to beat the test
• But I like the fact that number 2 is accusing number 1: "is cheater"!

Take a look at their statistics page where they show a histogram of 600,000 RTs that people generated in the last month

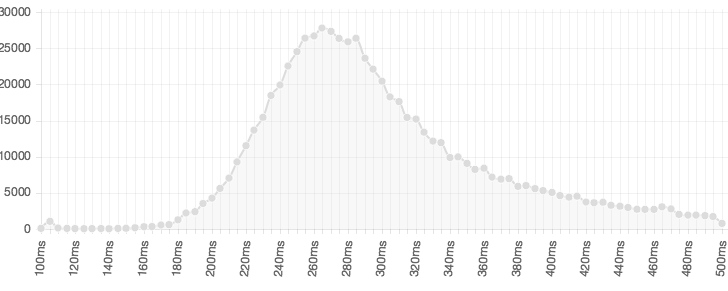
Where would your RT fall on this curve?

I captured the data from the image and made the into a text file, RT.txt.

• Download the data
• Load them into Matlab as a matrix called RT
• What do you think is in the two columns of RT?

  ?

  • Column 1 is the mean value for each RT 'bin'
  • Column 2 is the number of RTs recorded in this bin (so the y-axis could be labelled 'frequency')

• Can you make a plot of the data that looks similar to the one above?

?

>> plot(RT(:,1),RT(:,2),'o-');

Getting the mean and standard deviation

What are the mean and standard deviation of reaction times?

• To work this out you need to use the formula for expected value (the mean) in terms of :

  • Values (100ms, 105ms, etc)
  • Frequencies (405 suspect clicks at 100ms, 1198 suspect clicks at 105ms etc)

  ?

  mean = E(x) = Σ x ⋅ freq(x) ⁄ n

  Where x is the value of RT for a given bin, freq(x) is the frequency for that bin, and n is the total number of observations over all bins

• You will also need the equivalent formula for standard deviation

  ?

  standard deviation = √ (E(x²) - (E(x))²)

  Where you can work out E(x²) by plugging x² into the Expected value equation, instead of x.

Ok, tell me the answer!

?

>> Ex = sum(RT(:,1).*RT(:,2)) ./ sum(RT(:,2));
>> Ex2 = sum((RT(:,1).^2).*RT(:,2)) ./ sum(RT(:,2));
>>
>> m = Ex
>> s = sqrt(Ex2 - (Ex.^2))

Or if you want to unpack it further:

>> x = RT(:,1);
>> x2 = RT(:,1).^2
>>
>> freq_x = RT(:,2)
>>
>> n = sum(RT(:,2))
>> Ex = sum( x .* freq_x ) ./ n;
>> Ex2 = sum( x2 .* freq_x ) ./ n;
>>
>> m = Ex
>> s = sqrt(Ex2 - (Ex.^2))

Z-score your data

Now you know the mean and standard deviation, you can convert your RT into a Z-score.

The problem

RT data are notoriously non-normal.

What RT value is 2-standard deviations below the mean?

?

I make the mean 292 ms and the stdev 66 ms, so m-2s = 160 ms

What RT value is 2-standard deviations above the mean?

?

I make the mean 292 ms and the stdev 66 ms, so m+2s = 425 ms

How many RTs were recorded more than 2 stdevs below the mean?

?

>> ix = find(RT(:,1)<160 % find the rows with RT values less than 160
>> sum(RT(ix,2)) % and add up the frequencies for those rows

How many RTs were recorded more than 2 stdevs above the mean?

Clearly, for these non-normal data, Z-scores do not tell us how unlikely a given observation is!

Log Transform

In the lognormal distribution, the log of the data values follows a normal distribution.

So if we take the log of each RT value, the resulting log transformed values log(RT) should be normal distributed.

Calculate the log-transformed RTs for the given data and plot them.

?

>> logRT(:,1)=log(RT(:,1))
>> logRT(:,2)=RT(:,2);
>> plot(logRT(:,1),logRT(:,2),'o-');

• Is the distribution roughly normal?
• What is the mean of the logged RTs? is this the same as the log of the mean of the RTs?

  ?

  The two values mean(log(RT)) and log(mean(RT)) are not the same.

  You can probably see why if you compare the plots of RT and log(RT).

  In the case of the rates themselves, the right hand tail is fatter than the left hand tail. In other words, there is a greater spread for high firing rates than for low firing rates. This drags the mean to the right.

  For the log-transformed RTs there is no such asymmetry.

• What is the standard deviation of log(RT)?

Hopefully you are convinced that the log RTs are close to being Normally distributed than the raw RTs were.

• What are the log-transformed equivalents of the RTs we found to be 2 stdevs above and below the mean?
• Can you find the Z-scores these log transformed values?

Hopefully, the Z-scores are no longer the same size. It is now apparent that the lower RT is more unusual.

Log transforming data is a common trick to make right-skewed data approximately normally distributed.

Probability Matching (no exercises in this bit)

Log transforming data is a helpful trick for making right-skewed, positive data more Normal.

There is a more general approach for mapping non-Normal data onto a normal distribution though: probability matching.

This image illustrates the concept of probability matching for two probability density functions (probability distributions adjusted so that the area under the whole curve adds up to 1).

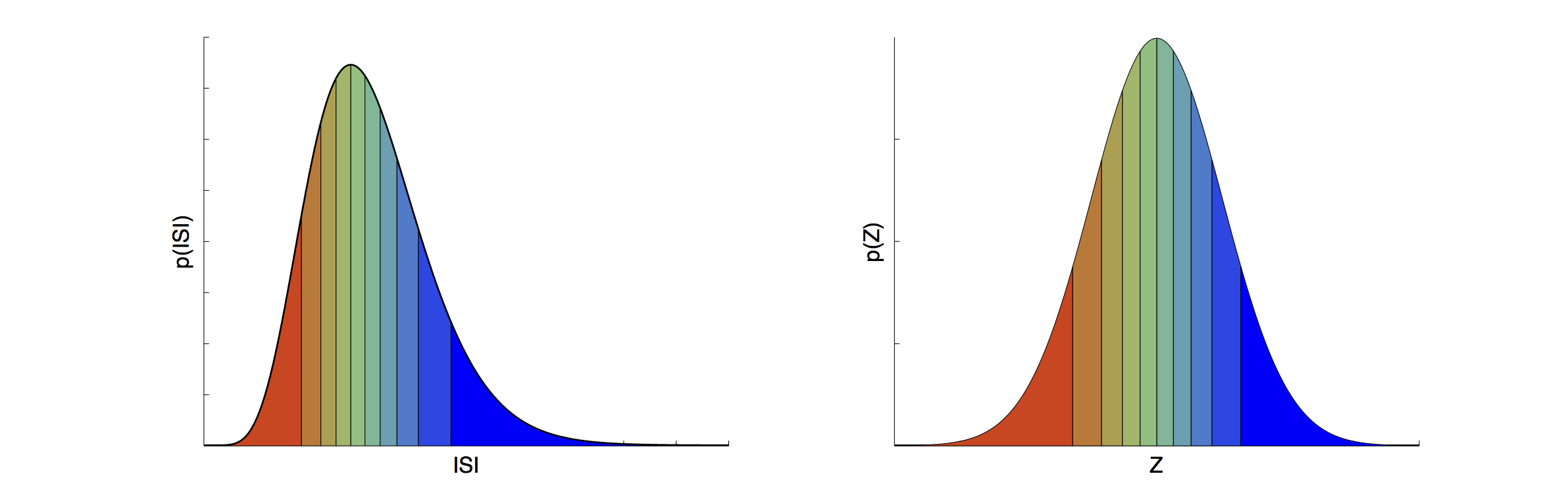
On the left we have a distribution of Inter-spike Intervals that is heavily right skewed. On the right, we have a Standard Normal Distribution.

For any probability density function, the area under the curve of the distribution, between two values on the x-axis, gives the probability of observing a data value in that range. In the case that we are looking at the area in the tail of the distribution (area under the curve from the edge of the distribution to some value X) the area under the curve is the same a the p-value for X.

I have sliced the probability distribution up into slices of equal area.

As you can see, the spacing of the slices on the x-axis is not even, and is not the same for the two distributions.

But hopefully you can see intuitively that the boundaries between slices correspond to the same p-values in both cases. So matching the boundaries between slices of equal area gives a natural "mapping" or transformation between the two distributions.

This is a Probability Matching transformation and is commonly used in data analysis packages - normally to convert non-Normal data to a Normal distribution so that Normal-assumption statistics like Z-scores and t-tests can be used.

For example, the Oxford fMRI analysis package FEAT makes use of probability transformations so that "activation levels" can be reported as Z-scores.

Extra Exercises

Pick and choose - you won't have time for all of them

Plotting Data

If you skipped the 'diversion' earlier and now have time, go back and do that exercise

You can find more material about plotting data in the MATLAB primer section on plotting data (Section 4).

• In particular, sections 4-2 to 4-15 would be relevant to what we did today.
• Section 4-19 shows you how to make some cool looking plots.
• The other stuff on saving figures etc is a little boring but is useful reference material (ie it's good to know where to find it if you need it, but you might not want to sit and work through it now).

There is more fun to be had in Stormy Attaway, chapter 11, including animations!

Writing functions in MATLAB

Can you write a MATLAB function zscore that takes in:

• a value x,
• population mean μ
• population standard deviation σ

and returns the Z-score, Z?

You can read about MATLAB functions in:

• The MATLAB Getting Started guide, section 5-11
• Stormy Attaway Chaper 3, especially section 3.7

If you are not sure how to tackle this, please work through that section first rather than just looking at the answer!

?

In a new script, type:

function Z = myzscore(x,mu,sigma)
Z = (x-mu)./sigma;

Save the script in the current working directory as zscore.m

You can test your function on Eric's data. If you do:

>> myzscore(195,179,7)

Do you get the answer you expect?

Probability Integral Transform (advanced)

I have thrown in a difficult exercise here on probability matching. This is more one for any computationally-savvy students who have whizzed through the rest already.

It is quite long so I have hidden it behind a click. Otherwise people reading the main text will get a false impression of how much there is to get through.

HIT ME!

Example: Inter-spike intervals

The distribution of inter-spike intervals is well-matched by a Gamma distribution. You may or may not have heard of the Gamma distribution, but here are some of its properties:

• It is a distribution over positive values
• It is right-skewed (fat right tail)
• It has two parameters, k and θ
  • The mean is kθ
  • The variance is kθ²
• ... so the variance is related to the mean.

Help, what are "parameters"??

In terms of probability distributions, you can think of it like this:

• A given distribution has a characteristic shape (like the bell-curve of the Normal distribution)
• But particular instance of this distribution is defined by input parameters
  • In the case of the Normal distribution, the parameters are the mean & #956 and standard deviation & #963
  • In the case of the Gamma distribution, the mean and standard deviation also depend on the input parameters k and θ, but somewhat less directly as the mean is kθ and the variance is kθ²
  • Another example of parameters is the parameters n and p of the binomial (coin-tossing) distribution (which gives the probability of obtaining k "heads" out of n coin tosses if the probability of heads on each trial is p (hopefully, 0.5!)

In other words, the Gamma distribution does not, in general, look at all like a Normal distribution.

Consider Inter-Spike Intervals (ISIs) that follow a Gamma(5,7) distribution.

Plot the probability of observing ISIs from 0 to 100ms using the function gampdf

HINT

How would you use normpdf to plot the probability of observing a Normal-distributed variable at values of 0-100, if the mean of the Normal distribution was 30 and the standard deviation was 5 ie, X~N(30,5)?

?

>> x=0:100 % x-axis values
>> y=normpdf(x,30,5); %corresponding y-axis values
>> plot(x,y);

By analogy, use gampdf(x,5,7) to plot the probability of observing a Gamma- distributed variable for values of 0-100 ie, ISI~Gamma(5,7)

?

>> x=0:100 % x-axis values
>> y=gampdf(x,5,7); %corresponding y-axis values
>> plot(x,y);

Generate 10000 random ISIs from the Gamma(5,7) distribution using gamrnd, which works a bit like randn although you have to tell it the parameters (5,7) of the Gamma distribution you are using. Don't forget that help gamrnd can help you with this!

?

>> ISIs = gamrnd(5,7,10000,1)

• What is the mean ISI? Is it close to kθ?

  ?

  >> mean(ISIs)

• What is the standard deviation?
• What is the variance? Is it close to kθ²?

Plot the ISIs in a histogram. Add the Gamma(5,7) distribution to the plot (matching its height so it fits nicely over the histogram, as we did earlier for the log-transformed spike rate data).

?

>> ISIs=gamrnd(5,7,10000,1);
>> hist(ISIs,40) % histogram with 40 bars
>> m1 = max(hist(ISIs)); % height of highest bar
>>
>> x = 0:100 % x-axis values
>> y = gampdf(x,5,7); >> m2 = max(y) % maximum height of Gamma distribution curve
>> y = y.*m1./m2 % Scale the Gamma distribution curve to match the histogram
>>
>> hold on;
>> plot(x,y,'r','LineWidth',2); % Use a thick, 2-pixel line

• What proportion of our sample of ISIs are less than 13.7 ms?

  ?

  >> sum(ISIs<13.7)./length(ISIs)

  The first part counts how many instances of ISIs less than 13.7 ms there are in our sample of 10 000. The second part divides by the number of samples (10 000) to make it into a proportion.

• What proportion of our sample if ISIs are over 64.1 ms?
• Are these values what we would expect from the Gamma(5,7) curve?
  • HINT: There is a function called gamcdf that works a bit like normcdf and tcdf, which we met in the sessions on Z-scores and t-tests respectively.

  ?

  >> gamcdf(13.5,5,7)
  >> gamcdf(64.1,5,7)
  

  The cdf functions (normcdf, tcdf, gamcdf etc) return the probability of observing a value less than the test value (e.g. 13.5 in this case) if the data follow the given distribution (Normal, t, Gamma) and parameters (& #956 = 0, & #963 = 1 in the case of the Standard Normal distribution eg normpdf(2.3,1,0); k=5,θ=7 in the case of the Gamma(5,7) distribution eg gamcdf(13.7,5,7))

  Put another way, the cdf functions tell you the area under the curve of the standardized probability distributions (Normal, Gamma etc) to the left of the test value

  

• Why do you think I chose those rather odd values?!

  ?

  They correspond to the values below- and above which (respectively) 5% of observations lie. So the probability of observing a value below 13.5 is 5% and the probability of observing a value above 64.1 is also 5% under the Gamma(5,7) distribution.

Converting between distributions

Say we conduct an experiment in which we expect the inter-spike interval of neurons to increase after application of a drug. We would like to know whether the drug has more effect on cell type A or cell type B, so we apply similar concentrations of the drug to cells of both types in vitro

In the absence of the drug:

• For cell type A, ISIs are well fit by the Gamma(5,7) distribution
• For cell type B, ISIs are well fit by the Gamma(4,6) distribution
• We know these distributions from prior work, or previous observations of our own

Plot the probability distribution of ISIs in the range 0-100 ms for each cell type, in the absence of a drug.

?

>> figure; hold on;
>> x = 0:100;
>> plot(x, gampdf(x,5,7), 'b') % cell type A
>> plot(x, gampdf(x,4,6), 'r') % cell type B
>> xlabel('ISI') % x axis label
>> ylabel('p(ISI)')

After applying the drug, I observe the following ISIs:

• Cell type A: [36 38 32 38 36]
• Cell type B: [25 26 28 26 23]
• Admittedly, it would be a bit lazy to only measure 5 ISIs in each case (since the total of the ISIs for cell type A is 180ms, it would be a short experiment!). This is just an illustration, OK?!

Which cell type shows a greater effect of drug?

One way to test this is to convert our ISIs into our favourite "common currency", Z-scores. But as they are not Normal-distributed, we can't just use the formula for Z. First we have to make them Normal distributed.

Here's the strategy:

• For each ISI x, calculated where it lies on the relevant Gamma CDF
  • i.e. the probability of observing an ISI less than x
• Find the value of Z for which p(an observation has a Z-score less than Z) matches the probability of observing an ISI less than x

That is our Z-score!

Do this for the observations from cell types A and B

• Abracadabra! our observations are converted into a common currency!

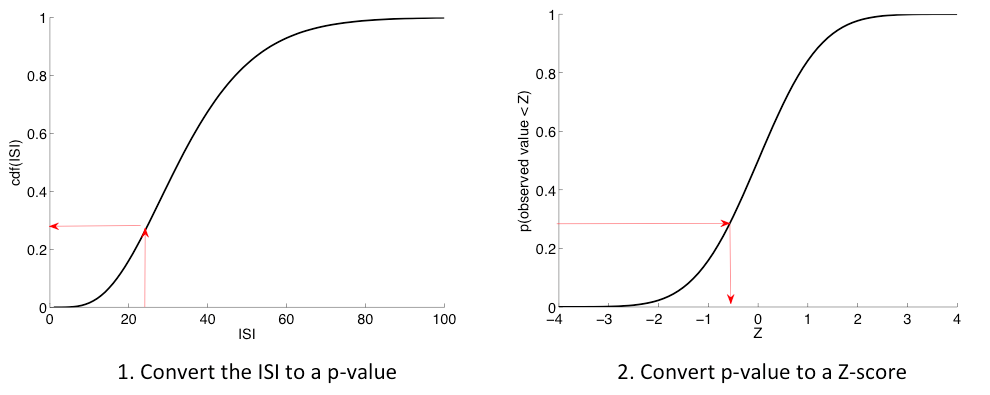And now in MATLAB. The key functions are:

• gamcdf(x,5,7) returns the probability of observing an ISI less than x, given that ISIs follow a gamma distribution with parameters k=5 and θ=7
• norminv, with parameters mean=0 and std=1, returns the Z-score relating to some probability value, such as the probability of observing an ISI less than x
• norminv(gamcdf(x,5,7),0,1) does it all in one go!

So, find the Z-scores for the ISIs in cell type A and B after application of the drug!

?

>> A = [36 38 32 38 36] ;
>> cdfA = gamcdf(A,5,7) ;
>> ZA = norminv(cdfA);
>> B = [25 26 28 26 23] ;
>> cdfB = gamcdf(B,4,6);% note parameters for ISI dist of cell type A are different from cell type A
>> ZB = norminv(cdfB);

Which cell type seemed more significantly affected by the drug in your opinion?

If you are unconvinced about this transformation business, it may help to apply the probability matching transformation to the whole Gamma distribution and check it comes out looking Z-like

>> x = 0:100;
>> G = gamcdf(x);
>> plot(x,G);
>>
>> Z = norminv(G);
>> plot(Z, normpdf(Z));