Data Analysis for Neuroscientists VI:
Advanced Regression

Recap: linear regression model

Last week we looked at how one variable (the response variable, y) can be predicted from another variable (the explanatory variable, x)

We fitted lines of the form:

$\hat{y} = mx + c$

But using slightly different notation:

$\hat{y}$ = $\hat{β}$ ₁x + $\hat{β}$ ₀

We also considered the residuals, y- $\hat{y}$ , which we assume:

Are Normally distributed
with a fixed variance that does not depend on the values of x and y

Putting this all together, we have a model in which we propose that our data y depend on the value of x, plus some contant, plus Gaussian noise:

y = β₀ + β₁x + N(0,σ²)

By a model, I mean a description of how our data y are generated.

Model ⇔ Data

Last time we looked at Galton's child vs. midparent data and fitted a linear regression model to them. Let's just do that again quickly.

Load the file parentChildHeight.txt, which contains:

the heights of parents, in inches, in the first column
the heights of their children, in inches, in the 2nd column

Fit a linear regression line to the data using glmfit

?

>> b = glmfit(data(:,1),data(:,2))

Plot the data

?

>> plot(data(:,1),data(:,2),'o')

Add the regression line to the plot

?

>> xvals = 63:73 % the range in x for which I want to plot my regression line >> yhat = b(1) + b(2).*xvals; % fitted y values >> >> hold on >> plot(xvals,yhat,'r');

Get the residuals by:

working out the predicted child's height $\hat{y}$ for each parent in the sample
and subtracting it from the true child's height y

?

>> data(:,3) = b(1) + b(2).*data(:,1); % fitted y values >> data(:,4) = data(:,3)-data(:,2); % residuals = yhat - y

Work out the standard deviation of the residuals

?

>> s = std(data(:,4))
I make it 2.24!

So we have a regression model in which the child's height y is predicted from the parent's height x, plus some noise:

y = 23.9 + 0.64 x + N(0,2.23²)

Different data, different model

Let's consider a different situation in which we again want to model a response variable y, based on some predictor variable x.

Consider an experiment in which participants view faces that are morphs between a fearful and angry facial expressions. Their task is to classify each image as fearful or angry:

If we code the response "angry" as 1 and "fearful" as 0, our data might look like this:

We would like to have some model that:

predicts the response y = (1 or 0) ...
...from the explanatory variable x = % angry face in the morph.

Can we use regression to solve this problem?

Linear regression won't work

Download the simulated data file FearfulAngry.txt, and load it into Matlab as data.

Let's try to fit a linear regression line

Column 1 of data contains the % angry morph on each trial

100% is pure angry face
0% is pure fear face

Column 2 contains the response on each trial

1 = responded "angry"
0 = responded "fear"

Use glmfit to fit a regression line

?

>> b = glmfit(data(:,1),data(:,2))

Plot the data and the regression line

?

>> xvals = 0:100 ; % x-axis values = % fearful >> yvals = b(1) + b(2).*xvals; >> >> figure; hold on; >> plot(data(:,1),data(:,2),'o'); >> plot(xvals,yvals,'r');

What problems do you notice with the regression line?

I can see a couple! HINT: Are all the data values it predicts possible?

?

The response can only take two values

1 = responded "angry"

0 = responded "fear"

... but the predicted line take all intermediate values as well

0.723 = responded "????"
...doesn't make any sense!

Also, the predicted line goes outside the range of responses -

what does a predicted response of 1.3 mean?

Back to the drawing board.

Logistic regression to the rescue

In linear regression, our model looked like this:

y = β₀ + β₁x + N(0,σ²)

In logistic regression, we use a different model:

Although this might look unrelated, note that:

Instead of fitting the value of y, we are fitting some function of y, that is p(y=1)

We are again fitting two coefficients:
- a constant β₀
- a coefficient of x, β₁
... but now instead of directly predicting the response variable, they are used in the exponent on the bottom of the fraction

The result is a regression line that is not straight but sigmoidal.

Fortunately, we can fit this sigmoidal line using glmfit. Let's try!

?

>> b = glmfit(data(:,1), data(:,2), 'binomial') % tell glmfit to use the binomial response distribution!

Now we can plot the data with the regression line:

First plot the data points themselves

?

>> plot(data(:,1),data(:,2),'o');

Then use the equation for the logistic curve to get the values of p(angry) for each x-value

?

>> xvals = 1:100 % x axis values >> p = 1./(1+exp(-1*(b(1)+b(2)*xvals)))

Plot it!

?

>> hold on >> plot(xvals,p)

Does it look like the actual outcomes follow the probability curve ?

Thinking point

Why is the sigmoidal, logistic regression line is more sensible than a straight line (linear regression) for these binary data?

?

With linear regression, we noticed we could get a prediction such as

y = 0.723
...which doesn't make any sense as y can only be 1 or 0

but with logistic regression, we accept that y = 0 or 1, but we can nonetheless predict the probability that it will take the value 1

The predictions is bounded by 0 and 1

so once we are certain the subject will respond "angry", no further change in the predicted response occurs, even if we make the face angrier and angrier

Arguably this reflects the nature of the data - if someone is responding "angry" 100% of the time for a given stimulus, we have reached a point where changing the explanatory variable doesn't change the response. So the regression line should flatten out.

Interpreting β₀ and β₁ in logistic regression

...is not straightforward

Since β₀ is a constant and doesn't interact with x, changing β₀ moves the logistic curve along without changing its shape

Try it out!

But changing the value of β₁ both changes slope of the line, and its location with respect to the x-axis.

Furthermore, we can no longer do a t-test on the regression coefficient. Instead we need to refer to the stats output of glmfit to find out if the effect of x on y is significant.

>> [b, d, stats] = glmfit(data(:,1),data(:,2),'binomial') >> stats.p % tell me the p-value for each beta

Applications of logistic regression

Logistic regression is important for predicting binary responses of all sorts

It is also used in machine learning. For example a simple classifier algorithm might take a training data set containing items of two types (e.g. images of cats and dogs) and fit a logistic regression curve to some features of those images (e.g., ear size) to try and predict which images are cats and which are dogs.

This prediction can then be tested in a new dataset to see if the boundary estabilshed using linear regression is robust.

Generalized linear model

Logistic regression is just one of a broader family of regression models called the Generalized Linear Model.

The Generalized Linear Model gives a framework for modelling relationships between explanatory variables and response variables, for various different data distributions.

glmfit stands for Generalized Linear Model fit.

Further Exercises

More on regression - for the enthusiast!

These are not in any particular order - the fMRI data is probably the most fun but fairly long.

Multiple regression

Often, our dependent variable depends on more than one independent, or explanatory variable.

Consider this very example: when an animal views a moving grating stimulus, the firing rate r of a magnocellular visual neuron depends on both the contrast of the current stimulus c, and its speed of motion s.

Then we can write the relationship in an equation as follows:

r = β₀ + β₁c + β₂s

In other words, we are now fitting r to a combination of two variables.

Say we know the values of β₀, β₁, β₂ and the equation is:

r = 5 + 8c + 3s

... where r is the firing rate in spikes per 10ms, c is the stimulus contrast (difference between brightest and darkest part of the stimulus, in lumens) and s is the speed at which the stimulus is moving in degrees of visual angle per second.

What is the firing rate for a grating with contrast 5 lumens and speed 4 °/s
?
>> c = 5; >> s = 4; >> r = 5 + 8.*c + 3.*s
What is the firing rate for a grating with contrast 10 lumens and speed 1 °/s
Say I would like to work out the firing rates for contrasts between 0 and 20 lumens in 1 lumen intervals, and all speed between 0°/s and 10°/s in 1°/s intervals.
How can I do this using two for loops?
?
>> c = 0:20; >> s = 0:10; >> for i = 1:length(c) % counter variable for c >> for j = 1:length(s) % counter variable for s >> r(i,j) = 5 + 8.*c(i) + 3*s(j); % now we are making a matrix of values for r >> end; >> end; >>
The fitted relationship is now not a line, but a plane. You can plot this using the function surf
?
>> surf(s,c,r) % surface plot
Play with rotating the surface to see how it looks from different angles. Of particular interest are the views where your line of sight is parallel to one of the axes, because these should allow you to see the relationship between c and r for different values of s, or the relationship between s and r for different values of c.

Finding the regression coefficients

Load the data Mcell_rate.txt. This file contains three columns:

Column 1 contains contrast values
Column 2 contains speed values
Column 3 contains firing rates

In this case, you don't know the values of the regression coefficients β₀, β₁, β₂, so you need to fit them to the data.

Plot the data on a 3D scatter plot using the plot function scatter3
?
Don't forget to check help scatter3!
?
>> data = load('MCell_rate.txt'); >> c = data(:,1) % contrast in column 1 >> s = data(:,2); % speed in column 2 >> r = data(:,3); % firing rate in column 3 >> scatter3(s,c,r,'k.');
Fit the regression coefficients using glmfit as before.
?
>> b = glmfit([c s],r) % I'm regressing r on a 2-column matrix containing both c and s
What are the values of β₀, β₁, β₂?
Work out the fitted values of r, rfit, for values of c from 0-20 and s from 0-10, given the regression coefficients
?
>> c_axis_vals = 0:20; % range of contrast values for which I want to fit r c >> s_axis_vals = 1:10; >> for i = 1:length(c_axis_vals) % counter variable for c >> for j = 1:length(s_axis_vals) % counter variable for s >> rfit(i,j) = b(1) + b(2).*c_axis_vals(i) + b(3)*s_axis_vals(j); % now we are making a matrix of values for r >> end; >> end;
Add the regression plane to your graph using surf
?
>> hold on; >> surf(s_axis_vals,c_axis_vals,rfit) % surface plot

Linear relationship between y, and a function of x

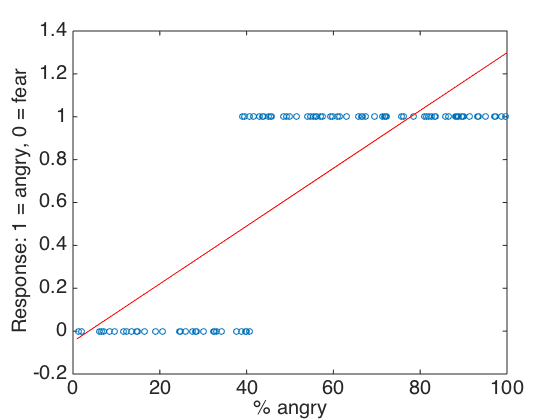
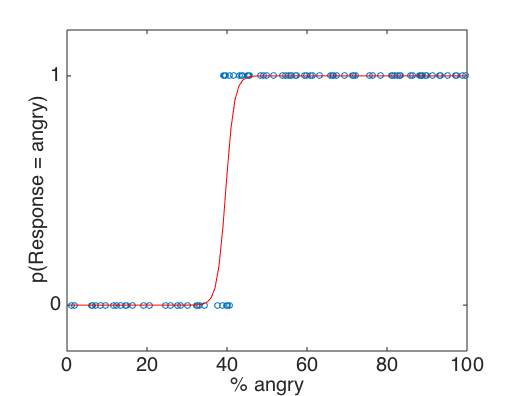
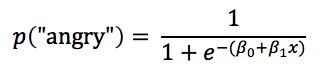Imagine we put a hungry rat in an operant box designed so that the rat has to press a lever a certain number of times to get a pellet of food.

We might propose a model in which that the number of times c the rat is prepared to press the level to get the pellet is proportional to the square root of the time t since it last ate.

For example say that:

p = 5 + 4

\sqrt{t}

Plot the predicted number of lever presses a rat will do, for times 0-12 hours after it last ate, at 30min intervals.

?
>> t = 0:0.5:12; >> p = 5 + 4.*sqrt(t); >> plot(t,p)

Now, load the data file leverpress_data.txt into a variable data. In the first column of this file, we have the time since last meal. In the second column, we have the number of leverpresses the rat performed.

Plot these data.

?
>> data = load('leverpresses.txt'); >> t = data(:,1); % times >> p = data(:,2); % number of presses >> plot(t,p,'.')

Hopefully, you can see that a straight-line relationship...

p = β₀ + β₁t

....between t and p is not going to be a good fit, especially at short time intervals.

Just out of curiosity though, fit one and plot the line on the graph.

?
>> ratstats = regstats(p,t) >> b0 = ratstats.beta(1); >> b1 = ratstats.beta(2); >> pfit = b0 + b1.*t; >> plot(t,p,'.'); hold on; >> plot(t,pfit,'-');

Replacing the explanatory (independent) variable

If we want to do fit a linear regression model to this data, how do we do it, given that y depends on $\sqrt{t}$ , not on t directly?

Easy! Define variable s = $\sqrt{t}$

Then we can write down our regression equation as follows:

p = β₀ + β₁s

Now if we plot p as a function of s rather than t, we should get a nice straight line!

For example say that:

p = 5 + 4

\sqrt{t}

Plot p against the square root of t.
?
>> t = 0:0.5:12; >> s = sqrt(t); >> p = 5 + 4.*s; >> plot(s,p)
or you could have just done:
>> t = 0:0.5:12; >> p = 5 + 4.*sqrt(t); >> plot(sqrt(t),p)
Fit a regression line to p and $\sqrt{t}$
?
>> b = glmfit(sqrt(t),p) >> pfit = b(1) + b(2).*sqrt(t); >> plot(sqrt(t),p,'.'); hold on; >> plot(sqrt(t),pfit,'-');
Plot the data p and the fitted values pfit against $\sqrt{t}$
?
>> plot(sqrt(t),p,'.'); hold on; >> plot(sqrt(t),pfit,'-');
Plot the data p and the fitted values pfit against t itself
?
>> plot(sqrt(t),p,'.'); hold on; >> plot(sqrt(t),pfit,'-');

Ta-da!!

What if an explanatory/independent variable is binary?

In some cases of multiple regression, one of our explanatory variables may be binary.

For example, say the firing rate of a cell depends on the intensity of a light stimulus, but also on whether the animal is paying attention to the light stimulus or not.

Then we can write the regression equation:

r = β₀ + β₁log(x₁) + β₂x₂

... where x1 is the light intensity and x2 is a binary variable that takes value 1 if the animal was attending to the light, and 0 otherwise.

Load the file attention_intensity.txt into a matrix called data

Column 1 contains the stimulus light intensity values, x₁
Column 2 contains the value of x₂ - whether the animal was attending or not
Column 3 contains the firing rate of the cell

Try plotting the firing rate against the light intensity, disregarding the attention variable.

?
>> data = load('attention_intensity.txt') >> plot(data(:,1),data(:,3),'.')

Hopefully, you can see that the data might be better fit by two regression lines than by one. This might be even clearer if you plot the "attended" and "unattended" stimuli in different colours.

?
>> data = load('attention_intensity.txt') >> att = find(data(:,2)==1) % find the rows corresponding to attended trials >> unatt = find(data(:,2)==0) >> plot(data(att,1),data(att,3),'b.') >> hold on >> plot(data(unatt,1),data(unatt,3),'r.')

Try fitting a regression model to the data, using glmfit as usual

?
>> betas = glmfit(data(:,1:2),data(:,3))

You should have three regression coefficients in the vector betas - the constant term, and the coefficients for the light intensity x₁ and the attention variable x₂.

Plus the regression coefficients back into the equation. Because this is a multiple regression, you could consider plotting the relationship of firing rate to x and a on a 3D plot. But because the attention variable is binary, you could also just add two regression lines, for the attended and unattended conditions, to your scatter plot.

?
>> b0 = betas(1); >> b1 = betas(2); % reg coeff for firing rate >> b2 = betas(3); % reg coeff for attention variable >> x_axis_vals = 1:100 >> rfit_att = b0 + x_axis_vals.*b1 + b2; % b2 is effectively a constant that we add on in attended trials >> rfit_unatt = b0 + x_axis_vals.*b1 ; >> >> plot(x_axis_vals, rfit_att, 'b-') >> plot(x_axis_vals, rfit_unatt, 'r-')

In summary, a binary explanatory (independent) variable is treated just like a continuous explanatory variable. But when plotting the data, you may not need to go for a full 3D plot, since the binary variable takes only two values (0 and 1) and so a 2D plot with 2 separate lines contains the same information as the 3D plot would.

The revenge of the fMRI data!

One application of linear regression is in fMRI analysis.

Typically, we would analyse fMRI data using a software package like FSL or SPM. These packages do all sorts of fancy stuff like pre-processing the data to improve signal to noise, registering to a standard space, correcting scanner distortions etc etc.

But the core of the actual statistics done by SPM, FSL and co is linear regression. I thought it might be informative to have a look at a linear regression in the context of the fMRI data we collected.

Remember in the fMRI practical, we asked our friendly volunteer to complete some sums of varying difficulty (adding numbers with 1, 2 or 3 digits).

The task was organised such that the volunteer did sums at one difficulty level for 15s, then rested for a few seconds, then did sums at another difficulty level for 15s. In fMRI analysis, we are interested in finding brain regions where activity varies over time, in synch with the difficulty of the sums.

Download the file sums_timings.txt and load it into MATLAB as a matrix raw_timings.

?
>> raw_timings = dlmread('sums_timings.txt')

Take a look at raw_timings. In this matrix we have:

Columns 1 and 2: The actual digits the volunteer added up on each trial
Column 3: The time the trial was presented, in seconds since the start of the experiment
Column 4: The difficulty level (1,2, or 3, meaning easy, medium or hard).

Make a graph with time on the x-axis, and one dot per trial, with y-value 1,2, or 3 for easy, medium and hard trials.

?
>> plot(raw_timings(:,3), raw_timings(:,4), 'o');

Now, I would like to model brain activity as being "on" during the blocks, and bigger on harder blocks.

Also, I have a measurement of brain activity only once every 3 seconds (due to the low temporal resolution for fMRI).

Download the file difficulty_blocks.txt and load it into MATLAB as blocks. In this file, I have put:

Column 1: the time in seconds at which each brain measurement was made (ie once every 3s)
Column 2: the difficult of the sums being done at that moment:
- 1,2,3 for easy, medium and hard
- 0 for rest blocks

Normally, FSL or SPM would generate this from the timings of the events themselves.

Plot the moment-by-moment difficulty given in blocks on the same graph as the individual trials. You might want to use a line, rather than dots, in this case, as we are modelling something that is continuous over time.

?
>> blocks = dlmread('difficulty_blocks.txt'); >> hold on; >> plot(blocks(:,1), blocks(:,2), 'b-');

Now, the BOLD response does not track the brain activity and the task in real time - there is a delay and smoothing factor caused by the Haemodynamic Response Function. I have therefore made another matrix (saved as difficulty_blocks_convolved.txt) which contains the time at which each brain measurement was made, and the predicted signal based on task difficulty convolved with the hrf.

Normally, FSL or SPM would make this for you.

Load difficulty_blocks_convolved.txt as blocks_conv and add the predicted signal to the graph, perhaps as a red line this time.

?
>> blocks_conv = dlmread('difficulty_blocks_convolved.txt'); >> hold on; >> plot(blocks_conv(:,1), blocks_conv(:,2), 'r-');

Hopefully you can see the relation between the three things plotted on the graph:

The actual trials
The blocks of (predicted) brain activity
The blocks of (predicted) fMRI signal after convolution with the HRF

Now it's time ot load up some fMRI data and run the regression!

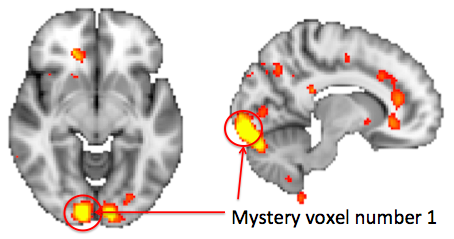
Normally, we would run the regression for each voxel in the brain, searching for voxels that are a good fit to our model (the red line on your graph). For the purposes of this tutorial, I have picked out a couple of individual voxels for you to have a look at.

Load mystery_voxel_1.txt as vox1. This file contains a column with the time at which the data were recorded (which should match the times in blocks_conv) and the BOLD signal from our Mystery Voxel at these times.

Start a new figure and plot the fMRI data against the time they were recorded.

?
>> vox1 = dlmread('mystery_voxel_1.txt'); >> figure; hold on; >> plot(vox1(:,1), vox1(:,2), 'k-');

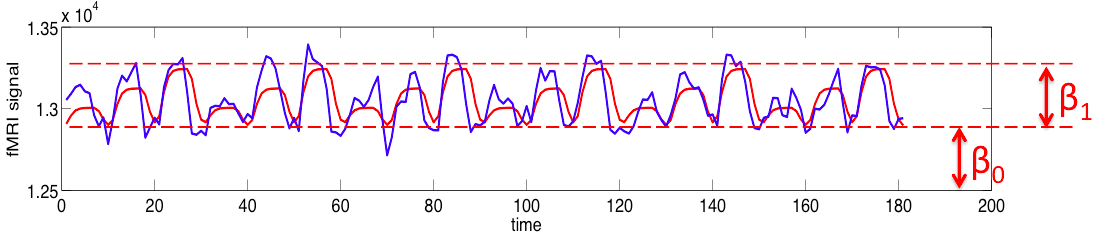
This looks hopeful! The BOLD signal does look a bit like our predicted signal blocks_conv. However, the actual y-values are really different - since the BOLD signal values are in the range 12000-13000, and the blocks_conv values are in the range 0-3.

Run a linear regression with blocks_conv(:,2) as the independent variable, and the fMRI data (vox1(:,2)) as the dependent variable.

?
>> b = glmfit(blocks_conv(:,2),vox1(:,2))

Find the predicted dependent-variable values $\hat{y}$ (the predicted BOLD signal) from the values of the dependent variable x (i.e., the values of blocks_conv) and the fitted values of slope β₁ and constant term/ y-intercept β₀
?
>> yfit = blocks_conv(:,2).*b(2) + b(1)
Add the fitted fMRI signal to the plot with the real fMRI signal
?
>> hold on; >> plot(blocks_conv(:,1),yfit,'r-'); % note the x-axis values are the times of the brain measurements
not bad eh?!

Data in this voxel were beautifully fit by the difficulty of the sums. Where do you think the voxel was in the brain? Maybe dorsolateral prefrontal cortex? Or perhaps the superior parietal lobule?

?

Uh-oh. It's the primary visual cortex!! Why would activity here fit the difficult of the sums so nicely?
HINT:

ANSWER: There was more visual stimulation for the 3-digit sums than the 1-digit sums. Oops!

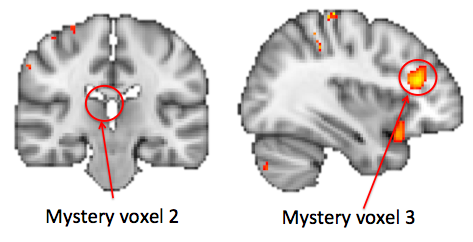
Fear not! I have provided two more mystery voxels, mystery_voxel_2.txt and mystery_voxel_3.txt. One of these is genuinely in the dlPFC and is genuinely interested in the difficulty of sums (although, sadly, with a lower significance level than the first Mystery Voxel). The other one is in the ventricle so should really not have any task-related signal.

Repeat the analysis procedure above and work out which mystery voxel is which!

?

You can copy the analysis steps from the previous Mystery Voxel!

Click here to reveal the locations of Mystery Voxels 2 and 3

Regression on timeseries vs. non-timeseries data

Now then - you may be thinking that the regressions we have done on the fMRI data don't look much like the regression in the first part of the tutorial.

In the case of the timeseries data, it looks like we are fitting the shape of some predicted signal (those blocks of activity of varying intensity) to the shape of actual brain activity over time.

How does this relate to the slope and y-intercept of a regression line?

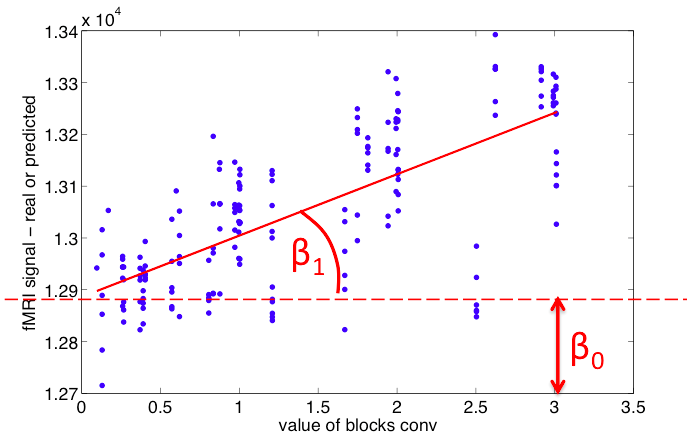
To understand this, it might help to just plot our dependent and independent variables for the fMRI data on a scatter plot, like we did for the simulated data in the first part of the tutorial.

Make a graph with the values of the independent variable, blocks_conv, on the x-axis, and the values of the fMRI signal vox1 on the y-axis.
Plot each data point as a dot on this graph
?
>> figure; plot(blocks_conv(:,2), vox1(:,2), '.');
You are only plotting the values of x and y at each timepoint -
so you only need the second columns of each matrix.

The first column just contains the times at which these data were recorded, which were used to match the x and y values to each other, but are now irrelevant.
Plot the regression line using the fitted values of the slope and y-intercept.
?
>> b = glmfit(blocks_conv(:,2), vox1(:,2)); >> x = blocks_conv(:,2) >> hold on; plot(x, b(2).*x + b(1), 'r-');

So the temporal regression of the fMRI data can be plotted just like an ordinary regression with a slope and a y-intercept. The relation between the two ways of looking at the data is illustrated below:

When doing regression on timeseries data, both of these ways of thinking about the regression can be helpful.

Data Analysis for Neuroscientists VI: Advanced Regression