Is it significant?

Typically if we observe a correlation between two variables, we want to know whether the correlation is statistically significant.

Usually our null hypothesis is that the true correlation in the population is zero

• ρ = 0

... and we would like to know how likely the observed correlation was, given the null hypothesis.

• What factors do you think should affect the statistical significance of the result?

?

• How different the correlation coefficient it from zero,
  eg r=0.7 more convincing than r=0.2

• Number of subjects the correlation coefficient was based on
  eg 50 subjects more convincing than 10

It turns out that we can calculate a t-value for the correlation coefficient using this formula:

?

...where t follows the t distribution with n-2 degrees of freedom

Is our correlation significant?

On the Matlab command line, enter the equation for t. Set the values of r and n to reflect the values we used in the sample.

?

>> r=0.24
>> n=50
>> t = r./sqrt((1-r^2)/(n-2))

The function tcdf returns the area under the curve to the left of some t-value.

• Use tcdf to find out if the correlation is significant

  HINT

  Have you tried

  >> help tcdf

  ?

  Reveal answer

  >> tcdf(t,48)

  We are using (n-2)=48 degrees of freedom

• If this value significant?

  ?

  I get a value of 0.9534 for the area under the curve to the left of t.

  Since we are looking at the right-hand tail of the distribution, this corresponds to a p-value of 1-0.9534=0.0464

  So the correlation would be significant at the 0.05 level, but not the 0.01 level, one tailed.

• Did you expect it to be significant from eyeballing the data?

  ?

  The effect looks rather weak when we plot the data, but remember significance depends on both the size of the effect and the number of subjects.

What does significance mean again?

What exactly does it mean if the p value is 0.05?

?

It means that

• if the real population correlation between x and y was zero
• we would expect to see a sample of size 50 with a correlation of 0.21 less than 5 times out of 100
• (if we repeated the experiment with 100 difference samples of 50, that is!)

Let's try it!

Generate 1000 samples from a population with ρ = 0, work out their correlation coefficients, and plot a histogram.

• You can do this using sections 2 and 3 of the provided script
• What proportion or samples have a correlation coefficient of 0.21 or greater?
• Add the t distribution you calculated above to the plot, to check it matches

Try it again with a sample size n=10 or n=100.

• For each value of n, how many sample correlation coefficients have r>0.21?

What is the critical r value for significance?

Finally let's work out exactly what the minimum r value would have been to give us a significant effect.

To do this we first use the function tinv, which gives us the critical the t-value corresponding to an input p value

?

>> tcrit = tinv(0.95, 48)

The help document help tinv may help!

I make it t=1.64

Then we need to find the r value corresponding to t=1.65

The problem is that it is not so easy to rearrange this formula:

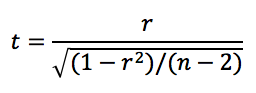
... to get r

Instead, I would suggest working out t for a range of r values, from the formula above, and finding the nearest t value to 1.64. Then take the corresponding r value as r_crit

?

>> rvals=-1:0.01:1
>> t = rvals./sqrt((1-rvals.^2)./(50-2))
>> ix = find(t>tcrit,1,'first');
>> rcrit = t(ix)

I make rcrit = 0.24.

►►►